The concept of cos(0) is fundamental in trigonometry and essential for various applications in mathematics, physics, and engineering. Whether you’re a student, educator, or professional, understanding this basic trigonometric function can be incredibly beneficial. In this article, we will delve deep into the meaning of cos(0), its significance, and its applications, providing a thorough and engaging exploration of this topic.
Key Takeway
Before we dive into the detailed content, here are the Key Takeaways about cos(0):
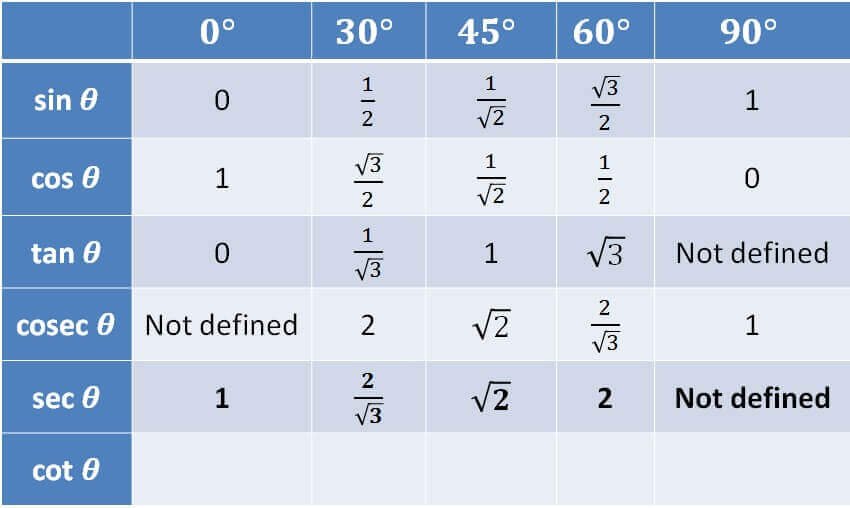
- cos(0) equals 1: This is a fundamental identity in trigonometry.
- Unit Circle: The value of cos(0) is derived from the unit circle, where the cosine of an angle is the x-coordinate of the corresponding point on the circle.
- Applications: Understanding cos(0) is crucial for solving problems in physics, engineering, and computer science.
Deep Dive
Who is Involved: Key Figures and Background Information
The concept of cosine, including cos(0), has been studied and refined by numerous mathematicians throughout history. Key figures include:
- Hipparchus: An ancient Greek astronomer and mathematician who is often credited with developing the early foundations of trigonometry.
- Claudius Ptolemy: Another Greek mathematician who expanded on Hipparchus’s work and compiled extensive trigonometric tables.
- Leonhard Euler: An 18th-century mathematician who made significant contributions to trigonometry and introduced the modern notation we use today.
Events Timeline: Important Dates and Milestones
The understanding and notation of trigonometric functions, including cos(0), have evolved over centuries. Here are some key milestones:
- 2nd Century BCE: Hipparchus creates the first known trigonometric table.
- 2nd Century CE: Ptolemy’s “Almagest” further develops trigonometric concepts and tables.
- 18th Century: Euler introduces modern trigonometric notation and identities, including the cosine function.
- 20th Century: The development of digital computers allows for the precise calculation and application of trigonometric functions in various fields.
Personal & Professional Impact
The understanding of cos(0) and trigonometry has profound implications for both personal and professional lives. Here are some examples:
- Education: Students learn about cos(0) early in their math education, providing a foundation for more advanced studies in calculus and beyond.
- Engineering: Engineers use trigonometric functions, including cos(0), to design and analyze structures, electrical circuits, and mechanical systems.
- Physics: Physicists apply trigonometric concepts to understand wave behavior, motion, and forces.
- Computer Graphics: Professionals in computer graphics and gaming use trigonometry to create realistic animations and simulations.
Press Reaction: Significant Coverage
While cos(0) may not frequently make headlines, its applications and implications are often discussed in educational and professional contexts. For example:
- Educational Media: Articles and tutorials on platforms like Khan Academy and educational YouTube channels frequently cover the basics of trigonometry, including cos(0).
- Professional Journals: Engineering and physics journals often publish papers that rely on trigonometric functions to explain new findings and innovations.
- Popular Science: Magazines and websites that popularize science occasionally delve into the importance of trigonometric functions in everyday technology and scientific research.
Upcoming Plans
The future of trigonometry and its applications, including the understanding of cos(0), continues to evolve. Here are some upcoming trends and potential developments:
- Advanced Computing: As computational power increases, the precision and application of trigonometric functions in simulations and models will become even more sophisticated.
- Educational Innovations: New teaching methods and technologies, such as virtual reality and interactive software, will enhance the way trigonometry is taught and understood.
- Interdisciplinary Research: The integration of trigonometry with other fields, such as data science and artificial intelligence, will open new avenues for research and application.
In conclusion, cos(0) is a fundamental concept in trigonometry with wide-ranging applications in education, engineering, physics, and computer science. By understanding the historical context, key figures, and practical implications of cos(0), we gain a deeper appreciation of its significance and utility. As we look to the future, the continued evolution of trigonometric applications promises exciting developments and innovations.
Whether you’re a student just starting to learn about trigonometry or a seasoned professional applying these concepts in your work, the value of understanding cos(0) cannot be overstated. Embrace this knowledge and explore the many ways it can enhance your understanding and capabilities.


